Orpheus: with the sixth generation, cease the glory of my song

The ancient Greeks were the first to discover and articulate a need for musical temperament. However, other forms of music evolved alongside tempered music without recognizing any such need. Music we might describe as indigenous or native is usually untempered and every bit as beautiful; in some ways, maybe more so.

This is the music we meditate to because it allows us to simplify, relax, and recharge: the music of Native America, of India and Indonesia — music we might describe as Eastern European, Asian, or Tartarian — is all considered to be natural and untempered music. 

[This article is also available as a video.]

Of course, we’re already familiar with Asia and Indonesia, but where was Tartaria? It’s been scrubbed from modern maps, but this Ortelius map, below, from 1603 shows Tartaria located in Asia, northwest of China, west of Mongolia, and east of Russia.

However, a set of stones referred to as the Tartarian tablets were found further west, in central Romania. Dr. Stephen Guide, in his book, The Thracian Script Decoded, discusses the Thracian Amulet of Tartaria, linking the ancient place names of Thrace and Tartary.

It was from Thrace that the musical demigod Orpheus emerged as the “father of songs.” He was believed, by the ancient Greeks, to be the greatest of all musicians, saying that his singing could divert the course of rivers and could enchant animals. The name of Orpheus is speculated to derive from the Greek word: órphnē (ὄρφνη), meaning darkness of the night, or darkness of the underworld. And this is the same meaning given to the place name of Tartaria or, as the Greeks called it, Tartarus (Τάρταρος), which was their place name for the hell that confined fallen angels.

The music of Orpheus was said to be enchanting and very pleasing to the ear. But oddly enough, the ancient Greek political philosopher Plato rejected the idea of tuning music by ear, as he illustrates in a conversation between Glaucon and Socrates in his book, The Republic (531a-d):

Or do you not know that they repeat the same procedure in the case of harmonies? They transfer it to hearing and measure audible concords and sounds against one another, expending much useless labor… preferring their ears to their minds…

Plato believed music could encourage lowly appetites and for this reason, he wanted music to be regulated:

But, even though they be not musical, those poems shall be sung which are composed by men who are personally good and honored in the State as performers of noble deeds. The adjudication of these shall lie with the Educator and the rest of the Law-wardens, who shall grant them the sole privilege of free speech in song; whereas to the others no permission shall be given; nor yet shall anyone venture to sing an unauthorized song…

To Plato, the untempered or Tartarian music of Orpheus represented a threat to the regulation of society. In his book Protagoras, Plato suggests that the music of Orpheus was a form of deceptive sophistry, the art of persuading people by giving them false but beautiful arguments. Plato saw Orpheus as someone simply enchanting the people with his beautiful voice. But music in ancient Greece was not meant for enjoyment. Its purpose was to program the people into consensus and to induce a war-like spirit in the soldiers. Plutarch explained this in his essay, “Concerning Music”:

[T]he ancient Greeks… were so careful to teach their children music. For they deemed it requisite by the assistance of music to form and compose the minds of youth to what was decent, sober, and virtuous; believing the use of music beneficially efficacious to incite to all serious actions, especially to the adventuring upon warlike dangers. To which purpose they made use of pipes or flutes when they advanced in battle array against their enemies… Others, even in our own times, continue using the trumpet.

I’ve included this information in my book, The Next Octave, and though it’s hard to imagine inflaming a warrior’s courage with harps, the ruling elites have used music throughout history to alter the psychology of their soldiers. For centuries, national anthems have been conditioning citizen populations into patriotic support for wars against the “correct” enemies. War is the ultimate expression of polarity and the right songs, in the right keys, using the right intervals, can inspire anger and a necessary “us vs. them” mentality. This is the ultimate purpose of regulated and tempered music.

So is it surprising that it was the Greeks who popularized the idea of Tartarus as the dark underworld of hell? This anti-Tartarian bias has existed all the way through the 19th century, where we find the word Tartar defined by Charles Mackay in 1888 as, “a great noise, clamour, bustle, confusion.”

The history of musical temperament boils down to a struggle between those who want to control people through sound, and those who wish to be musically free. The people of Tartary likely represented too much freedom, a concept Plato believed to be chaotic and licentious, and this is a theme that we find in his attempt to musically tune Atlantis.

In The Pythagorean Plato, Ernest McClain exposed hidden musical tuning systems encoded in much of Plato’s work. McClain believed that in portraying the four societies of Kallipolis, Athens, Magnesia, and Atlantis, Plato based each one on a method of tuning by which he could judge and compare their social and political success. The city of Atlantis was tuned with just intervals and its rings of land, separated by water, represented the Comma gaps between its untempered octaves. Plato then blamed the musical freedom of Atlantis, or its untempered musical chaos, for the fact that its society collapsed. At least, that was Plato’s underlying message.

The sixteen-note scale

One aspect of untempered music can be its use of the harmonic chromatic scale of 16 notes that I discuss in my book, The Next Octave. And musical instruments from the eastern area of Tartaria show the ancients using sets of 16 chromatic notes. How do we know these are sixteen chromatic notes and not simply two diatonic octaves? I’ll admit that we don’t know this for sure. But there is one clue.

When similar bells are arranged in a 12-note chromatic octave, the bells descend at an angle of negative four and a half degrees from tonic to octave. However, the two sets of eight bells in this depiction descend at an angle of negative two degrees and negative two and a half degrees, both of which add up to four and half and suggesting tones only descend by half the pitch. Meaning that from the tonic to the eighth bell, it’s only progressed half-way to the octave.

If this is the 16-note chromatic scale that it appears to be, I wonder if the conquest of Tartary and its erasure from history is a clue regarding the erasure from history of the 16-note scale.

I’m referring to the 16-note chromatic scale found between harmonics 16 and 32 in the harmonic series. To illustrate this, I’ll start by placing a regular C 12-note chromatic scale around a circle. At the left, is a line grid of the harmonic series, correlating each note around the circle to its harmonic frequency with a colored dot.

What you’ll notice is that every note in the scale correlates to a nice, evenly spaced harmonic on the left… except for one. The 27th harmonic that generates the note of A is offset from the rest of the scale, sitting much lower on the harmonic series than all the other notes.

The reason for this is that the harmonic series has stubbornly placed extra notes in between A and the rest of the scale, notes we don’t acknowledge or include in our traditional chromatic scale. But they do exist in harmonics 23, 25, 29, and 31, shown below in white. When these four phantom notes are included, we have a 16-note chromatic scale, which is likely what these early Tartarian instruments were expressing.

The use of a 16-note scale, and its harmonic tuning, may have allowed Tartarian music to circumvent the need for temperament — or squishing musical intervals — because the 16-note chromatic scale solves the problem of the Pythagorean comma — it generates a scale based on simple ratios and just intervals that also allows for a perfectly doubled octave.

Construction of the World Soul

But let’s look at how Plato suggested the creator of the world would tune music. In his book, Timaeus, Plato lays out the basic tuning of an octave in his story of how the demiurge constructed the World Soul:

And He began making the division thus: First He took one portion from the whole; then He took a portion double of this; then a third portion, half as much again as the second portion, that is, three times as much as the first; the fourth portion He took was twice as much as the second; the fifth three times as much as the third; the sixth eight times as much as the first; and the seventh twenty-seven times as much as the first.

This process was depicted by Crantor of Soli, a student of Plato’s, in what’s known as Crantor’s Lambda. The left side of Crantor’s Lambda is doubling, stacking octaves. The right side is tripling, stacking fifths, the same method of building a scale mentioned earlier that produces the problem of the Pythagorean comma.

If we build a scale by stacking fifths, we’re following the right side of Crantor’s Lambda. The lambda and the Circle of Fifths correlate because in the harmonic series, C is harmonic 1, G is harmonic 3, D is harmonic 9, and A is harmonic 27.

But it’s here that musical temperament is taking place, at least, according to McClain, because it’s here that the octaves are being filled with fifths and “tempered with thirds.” We can see how that’s done in this passage from Timaeus:

After that He went on to fill up the intervals in the series of the powers of 2 and the intervals in the series of powers of 3 in the following manner: He cut off yet further portions from the original mixture, and set them in between the portions above rehearsed, so as to place two Means in each interval, —one a Mean which exceeded its Extremes and was by them exceeded by the same proportional part or fraction of each of the Extremes respectively;

So let’s go over this in detail, because it’s not as difficult to comprehend as it might sound. Plato tells us that the demiurge filled the intervals with means. A mean is a point between two extremes: that exceeds its lower extreme (so it’s above it) and is exceeded by its upper extreme, so it’s below it. It will land somewhere within this interval, depending on what kind of mean it is:

Plato says that the first mean both exceeds and is exceeded by the same proportion. This is the description of a harmonic mean. The harmonic mean can be calculated by the formula of 2ab over [a] plus [b], and we’ll calculate it for the octave interval between 1 and 2 Hz below. That gives us the ratio of 4/3, the perfect fourth. On a piano, that would be from the note of C to the note of F.

Four divided by 3 is 1.33, so the harmonic mean between the octave of 1 and 2 is 1.33.  Is this a value that both exceeds and is exceeded by the same proportion? Yes, it is: the mean exceeds by 0.333, which is one-third of the first extreme, one. And the mean is exceeded by 0.666, which is one-third of the second extreme, two. The same proportion in each case is one-third.

If we stop right here, we find something extraordinary. It’s not mentioned anywhere in Timaeus, or anywhere that I’ve ever found, but it’s right there staring us in the face. By itself, this very first mean also solves the problem of the Pythagorean Comma.

Recall that when building a scale by stacking fifths, the octave C is calculated a bit sharp.

Looking more closely at this process, we see that the white keys of the C scale end with B before the black keys (the sharps and flats) start to be generated, and it’s with the black keys that the frequency values become fractional, or exhibit decimal places. But there’s one white key still to be calculated, the note of F, which waits until the very last position on the Circle of Fifths. If we use its calculated value of 345.99, the resulting octave of C will be 518.98, about 7 Hz sharp. But remember that Plato’s first mean generated an F on the left side of Crantor’s Lambda with a value of 1.333. If we scale that up to this octave between C at 256 and C at 512, the resulting F value is 341.333. Inserting this value for F into the Circle of Fifths, it’s the precise value we need to then generate a perfectly doubled octave at 512.

Boom, right? Problem solved. But nowhere that I’ve seen is this solution ever acknowledged. Instead, the demiurge simply moves on to fill more intervals with means.

Natural temperament

So Plato’s first meantone, the note of F calculated as a harmonic mean (1 1/3 Hz) within the 1-2 Hz octave of C, solved the problem of the Pythagorean Comma. But you might also be curious to know how the harmonic series solves the Pythagorean Comma, and the simple answer to that is with the 5th harmonic.

Remember that the right side of Crantor’s Lambda shows us the tripling process of stacking fifths. It starts out well, generating white keys with harmonic frequency values up through 27, which is the note of A. But if we extend the series down to the next number, that would be 27 tripled or 81, the note of E. As we’ll see, this is where the sharpness, the increased frequency of the comma begins.

The harmonic series does not generate the note of E with a value of 81. E is born into the harmonic series at harmonic 5, which scales up to a value of 80. And it’s this extra one hertz of frequency that begins the sharpness of stacking fifths. Instead, the harmonic series, placing E at 5, 10, 20, 40, and 80 Hz naturally reduces the interval enough to allow for the resulting C octaves to fit in the scale, perfectly doubled.

In my earlier video on the Phantom of the Opera, I show how the tension between harmonic E and Pythagorean E is encoded into the story, where Christine Daae represents stacking fifths and the E value of 81, while the Phantom represents harmonic 5, in the opera’s Box 5, and the E value of 80.

Proclus

But although we already have two solutions to the tuning problem of the Pythagorean Comma, Plato’s demiurge fails to look for a solution and continues on with his work of inserting means into the powers of 2 and 3:

After all the harmonic means are inserted (shown in pink), he begins on the arithmetic means, which calculate the mese of the interval (shown in orange). This process continues until 12 means have been inserted.

At this point, the focus shifts to filling the interval of the octave. The span of the first half of the octave runs from 16 to 24 (24:16 or 3:2) and the span of the second half of the octave runs from 24 to 32 (32:24 or 4:3).

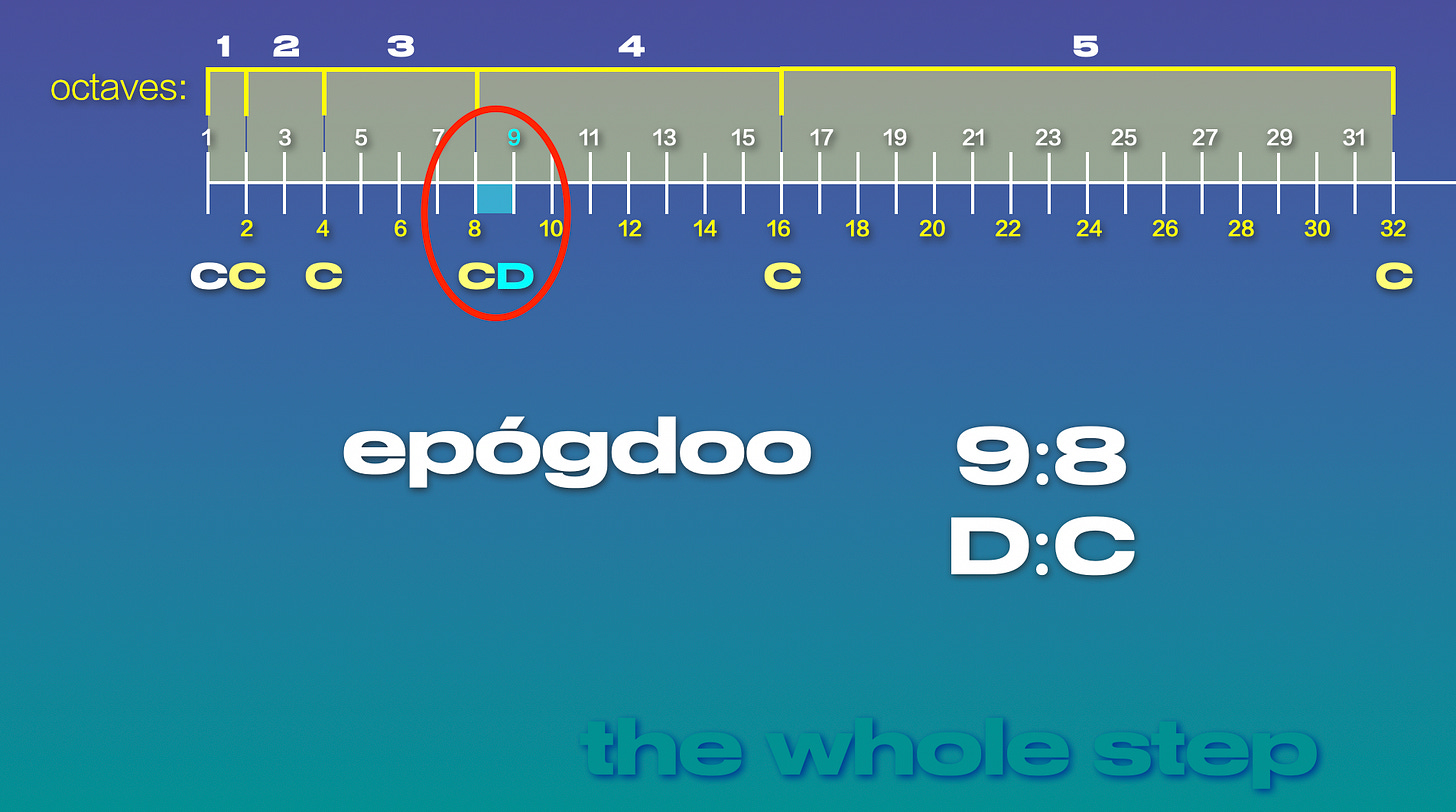
From here, according to Plato, the demiurge further divided these intervals using the epogdoo, the ratio of 9:8 that generates the whole step in a musical scale. In the harmonic series, the value of 9 is the note of D and the value of 8 is the note of C. So the ratio of 9:8 is really the ratio of D:C. We can better see this relationship between C and D below:

At the top, I’ve highlighted the first 5 octaves of the harmonic series, and we can also see that in these first 5 octaves, or first 32 harmonics, the note of C occurs six times, first as the tonic of harmonic 1, and then as octaves in harmonics 2, 4, 8, 16, and 32. But it isn’t until right after the C octave repeat at harmonic 8 that the D is generated in harmonic 9. And this space or interval between harmonics 9 and 8 is considered to be the just interval of a whole step.

This whole step ratio of 9:8 was called the epogdoo by the ancient Greeks, and it reveals a level of knowledge of the 16-note scale held by the Greeks that was not shared, taught, or utilized in their temperament of music. That knowledge was hinted at, however, by Proclus, a Greek philosopher who lived in the 5th century AD. He studied Plato and wrote several commentaries on his work. In his Commentary on Plato’s Timaeus, Volume 4, Book 3, Part II: Proclus on the World Soul, we read this: “the diatonic is composed out of the epogdoos [ratio] which 18 has to 16.”

Here, Proclus has scaled up the epogdoo from 9:8 to its octave at 18:16. And this is exactly the same whole step interval we find in the 16-note chromatic scale in the series. The only difference is that D has now scaled up to an even-numbered harmonic and the newly created harmonic 17, the note of C#, now exists within the 18:16 whole-step interval.

The fact that Proclus scales 9:8 up to 18:16 suggests he’s perceiving the octave not as partitioned into 8 notes, as a diatonic scale, but into 16 as a chromatic scale, of which C is the tonic. And he explicitly states this in his Timaeus commentary:

“…for the diatonic is composed out of the epogdoos [ratio] which 18 has to 16. On the one hand, the hêmiolios and epitritos ratios and the semi-tone are found among the other kinds of musical scales, but the epogdooi, on the other hand, are solely in the diachronic scale.”

Proclus is saying that the whole-step ratio of 18:16 is chromatic because there are 16 notes present—not 8, and not 12. And he explains his focus on the number 16 more fully, here: “It turns out that this ratio [18:16] probably makes the number of portions [16] that compose the scale in a manner that is just right…” (emphasis added)

This seems like an overt admission that the 16-note scale is the right or preferred scale. And yet, this represents the natural, and as we’ll see, ancient form of tuning we still find in native forms of music that the mathematicians and philosophers of Plato’s world rejected because this tuning wasn’t regulated. It was the unsophisticated form of tuning music enjoyed by barbaric people outside of Greek society, including the reviled Tartarians.

I’m sure most musicians today would disagree that the 16-note scale has just the right number of notes, because tuning with harmonic frequencies would produce intervals that aren’t used in mainstream music today. Man-made equal temperament is mainstream music. But while it’s true that harmonic tuning would create problems with changing keys, this natural tuning system provides the basic advantages of just intervals and simple ratios. The more we temper music, the more complicated the interval ratios become. And we can see this take place as Plato’s demiurge fills the octave interval of 4:3:

He’s filling the second half of the C scale, between notes of G and the next octave C. Between these notes, the demiurge is placing the notes of A and B a whole step apart, using the epogdoo of 9:8. However, the last interval between B and C is not a whole step. On the piano, we see that it’s a semitone because there’s no black key in between. The ratio Plato uses for this semitone interval seems pretty bulky (256:243) but it’s the only ratio that will fit. As we read in Timaeus, “This still left over a fraction which is represented by the terms of the numerical ratio 256:243.”

Let’s take a closer look at this ratio.

In the harmonic series, the frequency for Middle C just happens to be 256 Hz, so we can see that this is really the ratio of C:B, with B given the frequency value of 243 Hz. Because 243 is an odd number, that would mean that this slightly sharp B doesn’t enter the harmonic series until harmonic 243, well beyond the limit of harmonic 32.

In my book, The Next Octave, I discuss this limit of harmonic 32. Notes born after 32 aren’t really considered notes; they’re considered enharmonic means or microtones. And when a microtone like B at 243 forms an interval with a note established before the limit of harmonic 32, like C, the ratio can become much more complex or less clean and simple, less just.

Below, I’ve compared Plato’s tuning with harmonic tuning:

You can see that the ratio of 9:8 equals 1.125. But in the harmonic series, whole tones aren’t limited to just the 9:8 ratio. The interval from A to B is 1.11, the ratio of 10:9. It’s this difference that allows the final semitone ratio to be 16:15, a much cleaner ratio than Plato’s 256:243. The ratio of 16:15 is also the ratio of C:B because in the harmonic series, C scales up to 16, while B enters the series at harmonic 15.

Backward history of music

Looking back on the history of musical tuning, we find that man has actually been moving toward these complex, sophisticated ratios and away from natural, native tuning for thousands of years.

According to Richard Dumbrill, the co-founder of the International Council of Near Eastern Archaeomusicology, both the Sumerians and the Babylonians had written down note values for a D scale and we can compare three ancient scales, the Sumerian, Babylonian, and Greek to see the direction that tuning systems took.

The first scale was created in 2300 BC by mathematicians in Nippur who were reforming the earlier Sumerian scale. The values they calculated were identical to harmonic values with the exception of F# at 45, just one Hz above the harmonic F# at 44.

At least three centuries later, possibly more, the Babylonians calculated a similar scale. They also hit on several harmonic values, but their scale deviated from the series in two of its notes: again, the F# at 45, but also the C note at 1037 instead of 1024.  However, the Babylonians were at least sensing the need, in the key of D, for this note to be a C# rather than a C natural.

But several hundred years later, the Greeks were moving even farther away from harmonic intervals, tuning E at 81, F# at 729, and B at 243.

What’s interesting to notice, though, is that each of these ancient scales calculates A at 432 (the octave below 864).

And what we see here is that music tuning in Sumeria had it mostly right from the beginning. But as man attempted to perfect musical tuning, the ratios grew more complex, as tuning systems moved away from the harmonic values below 32 and up into the range of 45, 81, 243, and even 729.

Dumbrill produced the grid above the movement from the older Sumerian scale to the reformed scale of Nippur, explaining that they used both the just ratios of 9:8 and 10:9, as well as the just semitone ratio of 16:15. What’s probably most surprising here is that the Sumerians of Nippur were solving for the comma by adjusting E from 81 down to 80 — and all this several centuries before Pythagoras had even been born.

Orpheus & 6

Here in the west, we followed Plato’s lead and rejected Tartarian, native, or ancient musical tuning. As a result, where have we ended up? What are the ratios of equal temperament being used and broadcast today? As you’ll see, we’ve moved as far away from just intervals as possible under equal temperament.

We can’t blame Plato for equal temperament because it hadn’t been devised in his time, but he was definitely pushing us toward this modern environment of strict regulation and impinged freedom.

For the 3:2 and 4:3 intervals of the octave, equal temperament has adjusted these to the fractionted ratios of 3.062 : 2.043 and…. 4.087 : 3.062. And just in case you’re thinking that maybe this tempered 3:2 ratio might still be calculating something close to 1.5, this is the incredibly long decimal we now experience as our perfect 5th: 1.498776309348997.

It all seems to boil down to whether or not we honor the limit of the 32nd harmonic. Today, there is not one note on any piano that corresponds to a harmonic, whole-number frequency born into the series prior to harmonic 32. Only the notes of G and A exhibit whole-number frequencies at all, but in the case of G, its frequency entered the series at harmonic 49, and in the case of A=440, that entered the series at harmonic 55. In all of music today, the note of G is closest to just, and has been tempered the least. As a side note, many temperaments, including equal temperament, were calculated before computers and utilized a compass and straight edge.

But there’s an interesting bit of folklore, perhaps even Tartarian folklore, emanating from ancient Thrace that supports the concept of limiting our musical notes to the first 32 harmonics.

In Otto Kern’s “Orphic Fragment 14,” we find Plato, in his book Philebus, in which Socrates is quoting Orpheus: “And now, as Orpheus says, with the sixth generation, cease the glory of my song.” Many interpretations have been given for the possible meaning of this line, but I’d like to suggest another, in light of the fact that in the first 32 harmonics, the note of C is generated 6 times. That’s a total of 6 generations.