Harmonics and the conch shell

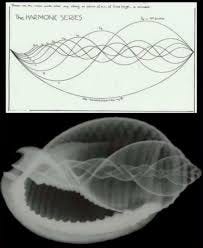
A popular internet meme loosely compares the sine waves of harmonic frequencies with the physical structure of a conch shell. I say “loosely” because if you really study the two images, you can see that there’s not a direct correlation.

Still, there’s an intriguing similarity here that I wanted to explore. And because I couldn’t find a sharp enough image of the harmonic waves on the top, I made my own. Below is an animated GIF I created to show how each wave overlays. They start and end on the assumed mese or center line, and once they’re all overlaid, you can see that the black waves all meet at the mese point on the mese line, marked with a black dot.

However, to make harmonic waves resemble a conch shell, those waves were all sized differently, top to bottom, reflecting various levels of wave amplitude. Using, instead, the same amplitude for each wave, the result looks nothing like a conch shell:

So that’s another “miracle” of mathematics destroyed.

I do think, though, that the overlaying of these harmonic waves is revealing something important involving the mese intersection, despite the brown waves shown above that fail to intersect it… or, perhaps, because of that failure.

Keep in mind that a complete sine wave is composed of two parts: half taking place on one side of the center line and half on the other. These two halves constitute one complete wave cycle.

So the first wave laid down in the animated GIF above is only half a wave, extending down from the mese line and returning to it, but not completing the wave’s second half above the center line. As such, waves on this graphic are colored brown if they’re fractions, like the first half-wave, and black if they’re whole numbers. As you can see, the four brown waves don’t meet the others at the mese point of the center line; only the black, whole-number frequency waves intersect the mese.

And this could have tangible implications regarding the effect of frequency on matter.

Before I saw this correlation between the whole-number frequency sine waves and the mese point, I believed that fractional frequencies were valid expressions of their larger octaves. Every note, every tone in existence has fractional octaves. Taking 432 Hz as an example, we know that this A note enters the harmonic series at Harmonic 27. One octave below that is 13.5 Hz, which should be just as beautifully intonated as every other octave of A=27.

And yet, there is no Harmonic 13.5. There couldn’t be because the harmonics that populate the series from Harmonic 1 to Harmonic 15 (and excluding the even-numbered octave repeats) are performing a structural function in preparation for the scale to come. Harmonic 13.5 wouldn’t fit into the structural expression of Harmonics 1 through 15.

In The Next Octave, I mention something important with regard to whole-number frequencies: “Formulated in 1900, Planck’s law, E=hv, describes the relationship between energy and frequency as proportional, where E is energy, v is frequency, and h is the Planck constant of 6.6 x 10^-34 joule seconds. This tells us that the energy of a photon is proportional to its frequency by a constant factor and only exists in multiples of whole numbers.”

Callum Coats restates this fact in Living Energies, his exposition of Schauberger’s theories: “Energy only exists in multiples of  whole numbers. The total action of energy is always a whole-numbered multiple of h.” This means there’s a palpable difference in fractional factors… therefore, the magic of 432 starts with the number 27, not 13.5.

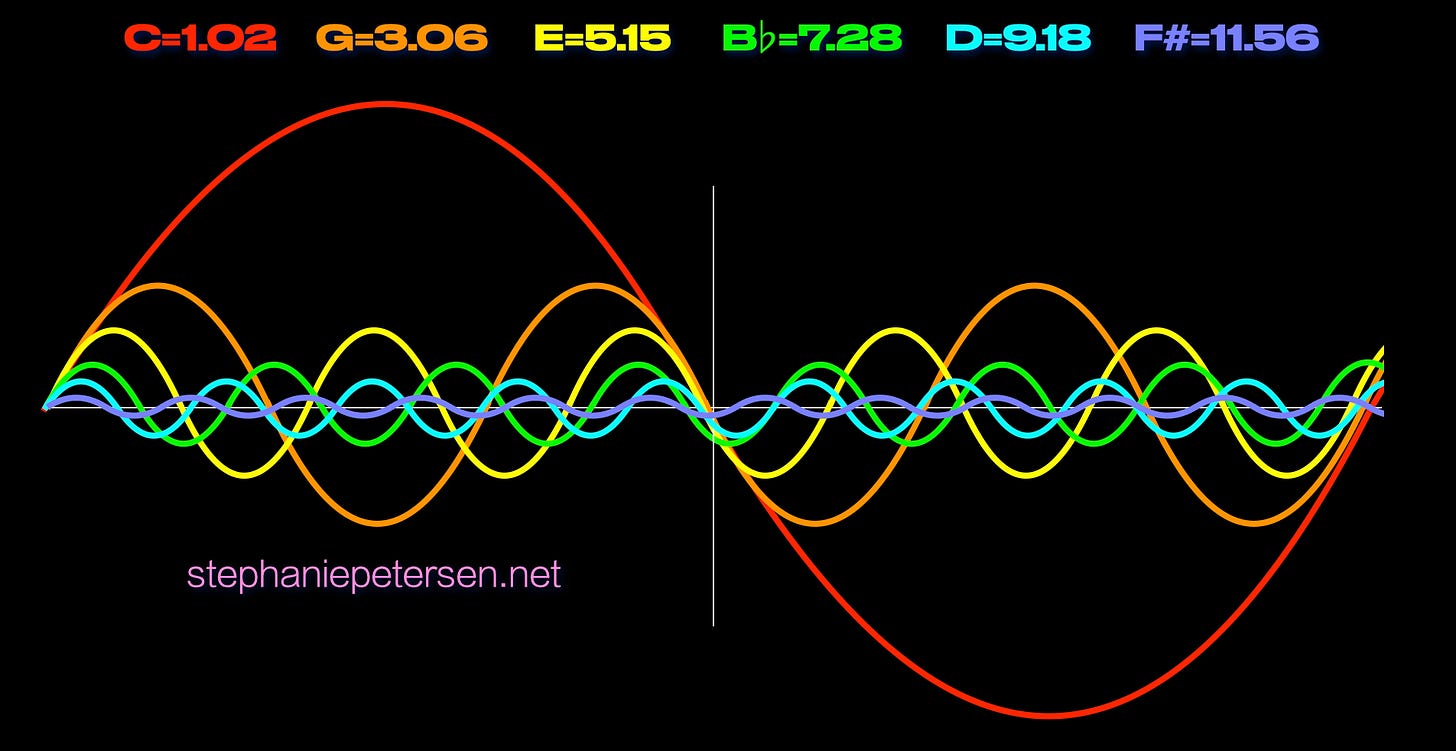
Below is a graphic I created showing the overlap of the first six harmonics generated in the series. If you’ve read The Next Octave, you’ll know that only odd-numbered harmonics represent new notes. (Even-numbered harmonics are simply octave repeats of the previously generated odd-numbered harmonics.) And I did stagger the levels of amplitude in order to separate these waves to see them more clearly:

The one common point through which all of these frequencies travel is the mese, and its importance can’t be overstressed. “Euclid calls Mese the sound by which all other sounds are regulated,” wrote Charles Burney in The General History of Music, published in 1776. “And Aristotle, in his XXXVIth problem, sect. 19, says that all the tones of a scale are accommodated, or tuned, to the Mese.”

The odd-numbered harmonics appearing above are all new harmonics, but they vary as reflecting either the power of 2 or 3: C=1, E=5, Bb=7 and F#=11 are all power of 2 values, with only G=3 and D=9 being power of 3 values. And yet both powers exhibit this “snapping to the grid” that’s regulated, even defined, by the mese.

If we then plot the frequency waves of the first four harmonic octaves of C, we see several points of intersection:

All four waves intersect the mese point, with smaller numbers of waves intersecting at equidistant points on the mese line: 3 waves at the quarter points and 2 waves at the eighth points. The energy being expressed here is regimented, but the odd-numbered harmonics, intersecting at only the mese, seem to be revealing something else… a complexity on the verge of cacophony, even noise, but regulated and harmonized by the centrality of the mese.

Octave intervals are musically uninteresting, with several points of intersection between waves. Music, though, requires more than octave intervals; it requires the varied, messy overlay of notes shown below. And when these various notes ring at precise intervals, the effect can be both healing and cacophonous. A balance must be struck, and that seems to be the purpose of the mese that draws the frequency waves together, if only for a moment, belting them at the waist before sending them out again into the vagaries of harmony.

Now, imagine a set of equally tempered frequencies that lack the regulatory feature of the mese. Here, I replaced the central dot with a thinner line to show that none of the waveforms of equal temperament actually intersect it:

To show a clearer comparison, I reduced the line thickness on these graphs from 9 down to 2 points. This allows you to see that equal temperament frequencies not only avoid the mese (miss the meson), they also fail to harmonically overlay one another.